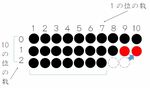
9の9倍、となったら9から1引いて8が10の位、残りは1で「81」自明じゃん、ということになる。
九九ならみなさん暗記しているわけですが、もう少し複雑な数の計算でも、この種の初等的な「定理」を証明して自明のものとしておけば、いちいち計算したり、ましていわんや、ばかばかしい暗記などせずとも、その場でサッと答えが出、かつ間違いないことは証明済みということになる。
お父さんの膝に乗せられ、もうそろそろ茹りそうなのに「9×8」がななじゅういくつだか丸暗記で思い出せない坊やは、
「9の段は暗記する必要がないんだよ」
の手品を知っていれば、さっさと湯舟から飛び出して、水鉄砲で遊ぶことができるわけです。
いま9の段を使いましたが、全く同様に8の段も7の段も、実は暗記する必要はありません。
でも暗記というか、すでに計算した結果をメモリに蓄えておくことは、高速処理の上で有利ですから、暗唱は依然としてお勧めなわけですが、算数の初歩といえども「丸暗記」は全く必要ないし、むしろ有害です。
その場で「7つの方法で導けるのが、頭を使うということの1の1になるんだよ」ってなことを教えてやる方が、はるかに涼しいことでしょう。
もっとまじめに続ければ、この先に初等整数論と呼ばれる、すべての数学の中でも最も美しい分野が、すぐさま姿を現します。
それは、掛け算割り算を教えた直後に素数と素因数分解を教え、ほんのちょっと、学習指導要領という救いようのない足かせを完全に無視することで、いとも簡単に実現できます。
高校数学を必修から外すなどという狂気の事態とまるで斜交いな、クールな眺望が開けることでしょう。
興味を持って取り組む子なら、小学校4、5年程度で、直後にビットコインの数理も完全に理解できるようになります。私自身、おいおいそういう教育をしてみようかな、と思っています。伸びたい人は来てみてください。
大学受験に情報科目でプログラミング能力がどうたら、という寝言があまりにくだらないので、純然と建設的なサンプルで、少しお話してみました。