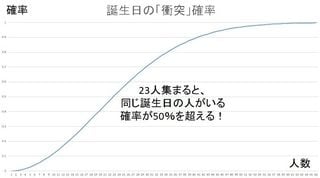
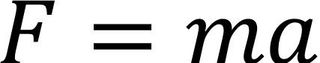実はこれは死んだ親が教えてくれた「9の段は足すと必ず9になる、なぜ?」なぞなぞの答えで、小学1年生の私には十分理解でき、また面白いものだな、と数理に興味をもつきっかけにもなった、懐かしいお話になります。
同じことを、もう少し学年の進んだ子に教えるなら、どうしたらいいでしょうか?
「別解」あるいは「別証明」を与えるという、数理の醍醐味の入り口を、子供に教えるいいチャンスになります。
例えば 9 というのは 9 でもありますが 10-1 とも 書くことができます。小学校高学年―中学生向けに 文字nを導入した「文字式」を使って原稿枚数を節約することにすることにして、9のn倍が「XY」という数だとしましょう。
Xは10の位、Yは1の位のつもりですから、正確には(X×10)+Yですが、以下では簡単に
「XY」=9×n=(10-1)×n
と書くことにします。ここでnは1、2、3、4、5… 9までの、一桁の自然数です。
この()の中を展開すると
「XY」=(10-1)×n=(10×n)-n
となりますから、n×10 から n を引いたことになる。ということは、10の位は必ず
n-1
になるので
X=(n-1)
であることが分かります。そこでこれを上の式に代入すると
(10×n)-n={10×(n-1)}+10-n
となり、1の位Yは
Y=10-n
そこで
X+Y=(n-1)+(10-n)=n-1+10-n=9
となり、nの値によらず、常に9になることが示せました。
こうなると、何が得かというと、もう九九の9の段は暗記しなくてもよいわけです。