子供向けに、玉の数を数えさせてみます。9つ一組の玉が2つある状況を考えて見ましょう。

ギャラリーページへ

　9＋9＝18　ですが　これを　9×2＝18　と考えさせるのが「掛け算」の導入になります。ケタをそろえて整列させると

ギャラリーページへ

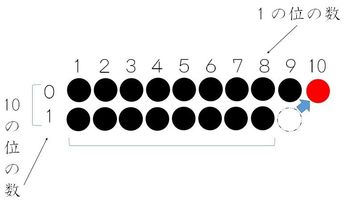
　2つ目のグループの9から、第1のグループに1つ移動して「10のかたまり」ができ、これで10の位が「1」（赤く着色した玉）。

　のこりが1の位にあたるので「9－1＝8」1の位は「8」。

　この「8」と、先ほどの「1」を足せば、確かに9になります。

　では「3・9＝27」はどうでしょうか？　もう一つ新たに9つ、玉のセットを導入しましょう（青く塗ってみました）。

ギャラリーページへ

　やはり整列させるには、10の位が「10のかたまり」になるのに、あと2つ「空席がありますから。その分を新しい9から移動してやればよく、10の位は「2」1の位は「7」

ギャラリーページへ

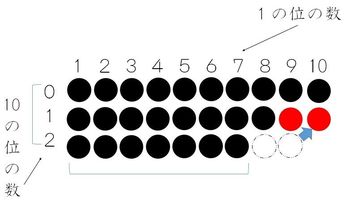
　「2＋7」で確かに9、つまり、新しく来た9から、何個か移動して10のかたまりを作ると、その移動した数と同じ「10の位」に必ずなるので、足せばもとの9になります。めでたしめでたし・・・。

　不十分ではありますが、でも一つの「証明」には違いありません。