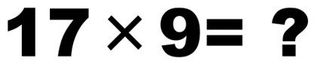ちなみに「トイレに入る」「チャックを下す」は、大学生向けに量子力学という科目を教えるとき、演算の非可換性を教授する例として私自身が東大生向けに普通に使ってきた例にほかなりません。

　さて、トイレから「さくらんぼ」に話を戻しますと

　小学1年生の子供は、上に示した「2つの解法」があることで「混乱」する、というのですね。これがいけません。

　そこで「さくらんぼ」表示をやめて、きちんとした数の式で記すことにしましょう。すなわち、第1の計算は

ギャラリーページへ

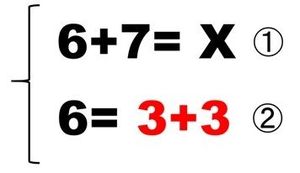
　元の式と、6＝3＋3　という式、2つを連立しているわけです。第1の式は未知数がある方程式、第2の式は常に成り立つので恒等式といいます。

　恒等式は常に成立するので、随時、様々な条件と連立することができます。

　高等学校の数学では、こういう計算テクニックを駆使する例が、因数分解でも不定積分でも＜難問＞とされる傾向があり、決してバカにはできません。

　この両者を連立すると、第1の「さくらんぼ計算」は以下のように書くことができます。

ギャラリーページへ

　これに対して第2の「さくらんぼ計算」は

ギャラリーページへ

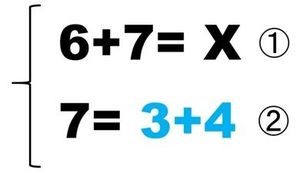
　この両者を連立して

ギャラリーページへ

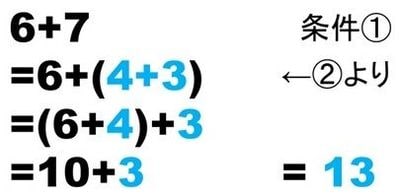
　このように解いている。演算としては、実は完全に同じことをしていますが、ポイントとしては、違う道順で解いている。ここがポイントになるでしょう。