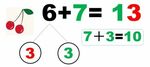
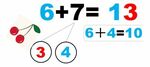
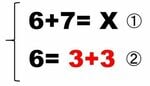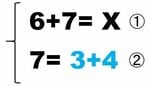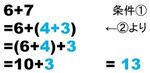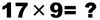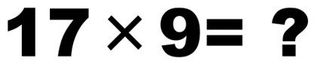この問題は、思うよりよほど根が深く、また数学の手技としては「telescoping(テレスコーピング)」と呼ばれる方法の初学者版になっているので、もう数回、紙幅を使ってきちんと議論したいと思います。
かつて徳川家康は「百姓は生かさぬように、殺さぬように」と語った、と江戸時代の兵法家大道寺友山は「落穂集」で伝えています。
その真意は、解釈が分かれるところかと思いますが、日本社会で一般庶民が身に着けるべき学問を「読み書きそろばん」に限定するというのは、典型的な「生かさぬように」の施策と言うべきでしょう。
税金を搾り取られる高を理解させる、というだけの知性で停滞する可能性が非常に高いと思います。
小学1年生向けにクイズよろしく、数の計算を一通りだけ教えるということに、私は強い疑問を持ちます。
一通り計算しても合っているかどうか分からない。「先生がマルをつけるか否か、あるいは模範解答と一致しているかどうか?」であれば、すでにそこには論理科学としての数学の品位は存在しません。
「数学の本質はその自由にある」というのは、集合論の始祖ゲオルグ・カントールの言葉です。ユダヤ系の出自で様々な冷遇にも接したカントールが、自律的なルール以外のすべてが自由である数理の美しさを端的に語ったものだと思います。
自分で出した答えが正しいか、怪しいか、自分自身で判断できるようになってこそ「百姓」は自立して生きる「ジェントリ」や「ユンカー」となって歴史を切り開いていけるようになるわけです。
小学1年最初の時点で「さくらんぼ検算」型の論理の自律性と美しさを教えることができれば何よりと思います。
ちなみに私は小学1年の1学期に、父親から手書きの九九の表を使って、算数は暗記の必要がほとんどないこと、「2×9=9×2」などの交換法則と対称性など、数理の美しさを教えてもらったことが決定的でした。
1学期の終わる7月12日に入院した父は、転移性肺がんでそのまま生きて帰宅することがありませんでした。
しかし、40数年経っても私の中にはヒト桁の数の演算挙動が示す美しさが、その先の高度な理論すべての原点としてハッキリ感じられます。
大切な論点と思いますので、引き続き取り上げたいと思います。
(つづく)