「さくらんぼ計算」を問題視する大人の中には
この2つの解法の「どっちがいいか?」といったことを巡って、あれこれ言う人がいるようです。
つまり、最初の計算に慣れている子にとっては、2番目の計算は混乱するだけだから「やめてくれ」であるとか、自分は第1の計算で慣れているので、第2の計算が出てくると「正直言って気分悪い」とか「ザラッとした気持になった」とかの反応です。
要するに、およそ数理とも論理とも関係のない、「自分にとって不快である」という意見が開陳されている。
これはつまり、小学1年生の足し算ですから、子供に質問されると、親も教えるわけですが、そこでおよそ非論理的な生活習慣をなぞることで、子供も混乱し、自分も不快になっているというのが実情なのではないか?
そういった感想を持ちました。
例えば「最初の数を【さくらんぼ】に分けるのに統一してくれ」とか「統一するのはけしからん」といった議論を目にしましたが、そういう向きには、「こういう問題ならどうなの?」と問うことになるでしょう。
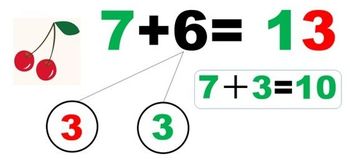
以下、大人の指導者向けに正確に議論を進めるべく、中学で習う数学の言葉を使ってお話を進めましょう。
足し算、つまり加算という演算には交換法則が成り立つので、6+7も7+6も答えは同じです。演算記号の前と後にある数字を入れ替えても、答えは変化しません。
(ちなみに除算つまり割り算では交換法則が成立しないので 6÷7と7÷6は答えが一致しません)
こういった、義務教育で教えているはずのシンプルだけれども厳密なロジックを、教室の先生も親も、徹底できていないように思います。