ニュートンの有名な言葉「リンゴも月も地球に落ちてきている」はどんな意味?物理学者・野村泰紀が語る物理学超入門
【著者に聞く】なぜ光は自然界で最高速度を誇るのか、アインシュタインの相対性理論に特殊と一般の2種類あるのはなぜ
2025.1.11(土)
ここからは、JBpress Premium 限定です。
カンタン登録!続けて記事をお読みください。詳細はこちら
あわせてお読みください

【物理学超入門】「光は波か粒子か」からスタートした量子力学、その歴史を物理学者の野村泰紀が語る
【著者に聞く】ホイヘンスにヤング、マクスウェル、プランク、ボーア、そしてシュレディンガー、続々と登場する物理界のスター
関 瑶子

折り紙でホイップクリームを作る?独自開発のソフトウェアと折り紙で無限のかたちを作り出す教授の突き抜けた発想
【研究って楽しい】折り紙をサイエンスにした筑波大学システム情報系・三谷純教授が語る、奥深すぎる折り紙の世界
関 瑶子

筑駒は、なぜ筑駒なのか?東大合格者を量産する国立大附属校のナゾ
【著者に聞く】進学校になったのはたまたま?授業は大学院レベル?共学化は?OBのAV男優が吐露するヤバさって?
関 瑶子

理論物理学が辿り着いたパラレルワールド的世界「私たちの世界は4次元でなく10次元、宇宙の数は無限」のホント
【研究って楽しい】カリフォルニア大学バークレー校の野村泰紀教授が語るマルチバース論(多元宇宙論)
関 瑶子

学級崩壊、教員の多忙化、理不尽な保護者、ブラックな学校を変える唯一の方法
「学びの共同体」、学校を開けば、教育が変わる、社会が変わる、未来が変わる【JBpressセレクション】
関 瑶子
イノベーション バックナンバー

唾液が認知症やがんの医療を変える!わずか1mlで早期発見が可能に、パーキンソン病など発症前からリスク判定も
竹林 篤実

AIでペットの気持ちが本当にわかるのか? 哲学者が考える「根本的な問い」とは
シンクロナス編集部
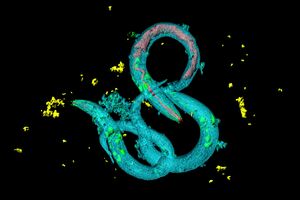
線虫の「老化」にみる驚くべき種の生存戦略、生殖機能がなくなったら集団のために自ら身を引く?
竹林 篤実

進化する“AI音楽”。生成AIが音楽シーンにもたらす変化とは? アメリカでは訴訟や法案提出も
シンクロナス編集部

ピンピンコロリの達人、ハダカデバネズミに学ぶ理想の生き方〜なぜ、老いもせず、衰えもせず、がんにもならないのか
竹林 篤実

なぜ国や自治体が惑わされる? 巧妙な「疑似科学」への向き合い方
シンクロナス編集部



