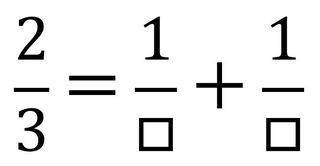エジプト・ルクソール近郊の「王家の谷」にある古代エジプトの王ツタンカーメンの地下墓地で展示されるひつぎ(2016年4月1日撮影)。(c)AFP/MOHAMED EL-SHAHED 〔AFPBB News〕
算数(単位分数分解)
社会(古代エジプトの民主主義)
先日、あらゆる有理数(分数のことです)は「単位分数」で表現できるという「フィボナッチ=シルヴェスターの定理」をご紹介したところ、思った以上に大変多くの方に読んでいただくことができました。
その続きをお話ししましょう。
「単位分数」というのは、分子が1であるような分数を指します。例えば「1/2」「1/3」「1/4」「1/5」・・・などなど。
こうした「単位分数」の足し算だけで、あらゆる分数を表現できる。こんな基本的な「数」の性質を、私たちはほとんど知らずに生活しています。
普通に大学を理系で卒業した人でも「単位分数分解」の事実を知らない人の方が多いのではないでしょうか?
理由はハッキリしています。「教育指導要領」に含まれていないから。
算術でも、幾何でも代数でも、どんなに基本的な性質であっても、日本の初等中等教育では、指導要領に含まれていない内容は一般に学校で教えられませんし、またそれを前提とする大学入試問題なども出ない。
入試に出ない、となると、多くの生徒と、それ以上に、そのスポンサーである親御さんも含めて「興味を持たない」という、非常に困った傾向が率直に言ってあるわけです。
これが何かの「役に立つ」となると、いきなり興味を持つ人が増える。
「何も得しない」となるとサッと潮が引くように興味が持たれなくなり「知らないと損をする」となると、突然黒山の人だかりになったりもする・・・。