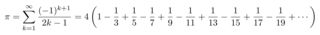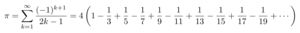・・・
11枚の画像を見る

関孝和の業績

 関孝和が算聖と讃えられるほどの業績を残しました。前回の傍書法はその1つに過ぎません。

 傍書法（代数式の表し方とその計算法）、ホーナー法（多変数高次方程式の解法）、方程式の判別式、ニュートン法、零約術（近似分数）、不定方程式の解法、招差法（階差を用いた未定係数決定法）、正多角形に関する関係式、円理（円周率の計算）、ニュートンの補間法、球の体積、ハップス・ギュルダンの定理、円錐曲線論、方陣の一般論、授時暦の研究、…

 これら関孝和の数学の全貌を紹介することは困難を極めます。それでもなお関孝和の偉大さを伝えるために、業績の一端を紹介してみようと思います。

 ここでは、世界に先駆けた関孝和の発見を2つ取り上げます。

関の公式その１ 関・ベルヌーイ数

 自然数のべき乗をたし合わせる公式は総和公式と呼ばれます。高校数学の教科書に登場するのは次のようなΣを用いた公式で、数列の部分がkの1乗、2乗、3乗である場合です。

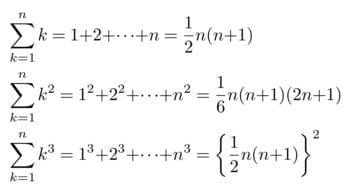高校数学で習う総和公式
ギャラリーページへ

 すると、k の4乗、5乗、…と考えて、一般にp乗の場合の公式を考えることができます。

ギャラリーページへ

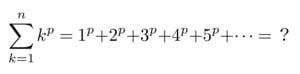
 総和公式の一般化に初めて成功した数学者こそ、われらが関孝和（1640？-1708）とスイスが生んだ世界的数学者ヤコブ・ベルヌーイ（1654-1705）です。

関孝和（1640？～1708）
ギャラリーページへ
ヤコブ・ベルヌーイ（1654～1705）
ギャラリーページへ

 驚くべきことが2つあります。2人が同時期に研究を行っていること、そしてその研究の中身も同じであることです。

 2人とも法則を見つけるために、kの4乗、5乗、…、10乗までの場合の総和公式を計算しています。

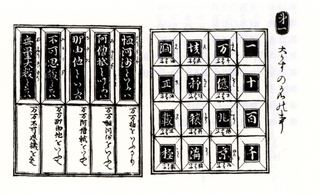
 『括用算法（かつようさんぽう）』（1712年）と『Ars Conjectandi（推測術）』（1713年）の中で発表されました。次が両者が10乗までの場合の総和公式を計算している該当部分です。