フォロー
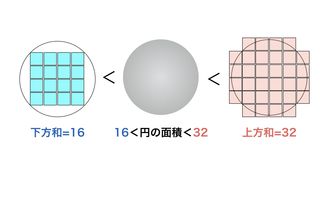
独エッセンで観測された月食が始まり赤く染まる月（2015年9月28日撮影）〔AFPBB News〕
ギャラリーページへ
マダヴァ・グレゴリー・ライプニッツの公式
Σの呪縛を解くシリーズ第7弾のテーマはπ公式の鑑賞です。
前回、「Σの数式を鑑賞するおもしろさ」として数学公式集を紹介しました。今回はπ公式です。
π公式はΣの数式のオンパレード。これまでの連載でもπを何度も取り上げてきましたが、今回はπ公式の中からΣの数式だけを選んでみました。
一般には「ライプニッツの公式」と呼ばれる公式は1674年にライプニッツ（1646-1716）によって発見されたものです。正式名称は「マダヴァ・グレゴリー・ライプニッツの公式」と呼ばれます。
その由縁を追ってみます。
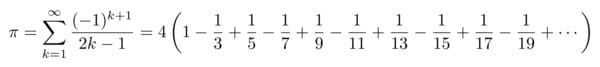マダヴァ・グレゴリー・ライプニッツの公式
・・・
14枚の画像を見る
この数式を見たライプニッツは「ここに神がいる」と叫んだと言います。なるほど、このπ公式は見れば見るほど魅惑的なシンプルなフォルムをしています。
ライプニッツの数年前1671年にスコットランドの数学者、天文学者グレゴリー（1638-1675）が次の公式を発見しました。
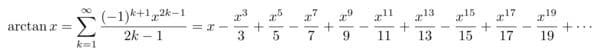グレゴリー級数ギャラリーページへ
ニュートン（1642-1727）と同時代を生きたグレゴリーによるこの公式は微分積分学初期の成果と言えるものです。ライプニッツはこのグレゴリー級数にx=1を代入することに気付きました。なぜならtan 45°=1だからです。
45°を弧度法で表すとπ/4なので、次が成り立ちます。
ギャラリーページへ
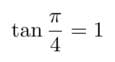
このtanの式のπ/4と1の関係を逆にしたのが次のarctanの式です。
ギャラリーページへ
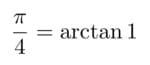
arctanのarcとは弧という意味で、正接関数tanに対して逆正接関数と呼ばれます。上の式はtanの値が1となるような円弧の長さがπ/4であることを表しています。こうして、ライプニッツは冒頭のπ公式を導きました。
