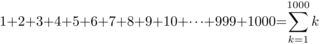フィリピンの首都マニラ北方のパンパンガで開催された国際熱気球フェスティバル(2017年2月9日撮影)〔AFPBB News〕
Σ記号=たし算命令指示書
Σの呪縛を解くシリーズ第2弾。前回「1から10万や奇数、偶数を簡単にたし算する方法」では、Σの呪縛を解くカギが「図形」でした。今回のカギは「見つめる」です。
Σ記号とは言うならば「たし算命令指示書」です。
4つの指示──「変数」「始まりの整数値」「終わりの整数値」そして「数式」が明記されると、「変数の値を始まりの整数値から1ずつ増やして終わりの整数値まで順に、数式に代入してすべてたし算せよ」という内容になります。
もし、4つの指示がそれぞれ「k」「1」「4」「2k」であれば、「kの値を1、2、3、4と順に、数式2kに代入してすべてたし算せよ」となるので、「2+4+6+8」を表します。
「変数」は整数値をとることがΣのルールです。ですから変数にはi、j、k、l、m、nといった数学で整数値を表す文字が用いられます。
"苦役"だったΣ公式の計算練習
そして、「Σ公式」とは、「始まりの整数値」を1、「終わりの整数値」をnとした場合の総和をnで表した式のことです。例えば、4つの指示が「k」「1」「n」「k」の場合のΣ公式は、1+2+3+…+n=n(n+1)/2です。
これから、4つの指示が「k」「1」「n」「2k」の場合のΣ公式は、2+4+6+…+2n=n(n+1)と分かります。
「Σ公式」を用いれば、「たし算命令指示書」の結果は、nに「終わりの整数値」を代入するだけで得られることになります。先の「2+4+6+8」の結果は、このたし算を実行する代わりに公式「n(n+1)」のnに「終わりの整数値」である4を代入して4×(4+1)=20と得られます。
「Σ公式」は「始まりの整数値」1から「終わりの整数値」nまで順に、「数式」に総て代入した和を求めるものなので、総和公式とも呼ばれます。
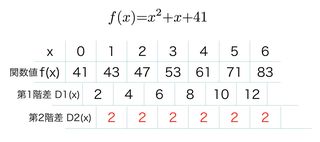
高校数学の教科書には、数式がk、kの2乗、kの3乗の総和公式が登場します。はたして、総和公式(左辺がΣの式、右辺がnの式)を使った計算練習が"苦役"のごとく高校生に要求されます。Σという「たし算命令指示書」に従い、面倒なだけのnの計算。こんな計算に興味が持てるはずがないじゃないですか!
前回も言いましたが、Σの本来の目的はたし算です。"苦役"から受ける印象はたし算どころか何をしているのかさえ分からなくなる酷いものです。
まさしく「苦役に耐える」だったのです。いったい、「Σ」を見るとフラッシュバックのように"苦役"が思い出される人がどれだけいるのでしょうか。
「たし算命令指示書」としてのΣの計算は苦役ではありません。苦役なのはΣの式のたし算を本当に実行することです。
もし「終わりの整数値」が10000と指示されれば、変数に1から10000まで順に代入してたし算を行わなければなりません。そもそもΣ記号がなければ10000項のたし算の式を筆記するだけで重労働です。ましてやそのたし算を実行するなんて!