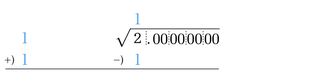ドイツの半導体メーカー、インフィニオンテクノロジーズ製のCPU〔AFPBB News〕
数表を作り続ける人類
数値計算をテーマに連載は続いてきました。連載「知って得する、いかに早く計算するか」では、多項式の数値計算に必要なかけ算の回数を減らすホーナー法を取り上げました。
連載「電卓遊びが導いた数値計算の世界」では、私が小学生の時に遭遇した電卓の謎(√とsin)が、高校生の時にマクローリン級数を知って解決していった思い出を語りました。
連載「知っておきたい平方根の計算方法」では、平方根の3つの数値計算法を紹介しました。そして、連載「対数表は紙計算機」では、対数表の数値計算の進化の風景を紹介しました。
ネイピアの20年に及ぶ計算、ネイピアの後を継いだブリッグスの平方根の計算を24回繰り返し行う方法、オイラーによるマクローリン級数を工夫した計算。
4000年前の古代エジプトに始まる三角法の歴史は、三角関数表作成とともに発展してきました。古代ギリシャのプトレマイオス(83-168)、15世紀ドイツの天文学者レギオモンタヌス(1436-1476)、16世紀オーストリアの天文学者ゲオルク・レティクス(1514-1574)らが脈々と三角関数表を作り上げてきました。
我が国での最初の三角関数表は江戸時代の数学者建部賢弘(1664-1739)によって作成されました。
そして、天文学と航海術における三角関数表は、時代を追うごとにその精度が高くなっていきました。三角関数の計算克服のために誕生したのがネイピアによる対数表だったことは連載「ジョン・ネイピア物語~対数は天文学者の寿命を2倍にした」で紹介した通りです。
人は死して数表を遺してきたということです。遺された数表のおかげで後世の人々は、計算のための時間を節約することができたわけです。
ネイピアの対数表から200年後、天才出現
ところが、数表の精度が高くなることは新たな問題も引き起こすことになります。ミスがない数表を作ることの困難さです。理由は単純で、すべての計算は人間の手によるものだったからです。
計算道具といっても、18世紀のヨーロッパではネイピアの計算棒(九九表を印字した棒)や算盤だけでした。
「computer」とは元々計算する者という意味ですが、「コンピューター」が計算したものを印刷工が活字を組んで印刷することで数表は作成されます。そのすべてのプロセスでミスが生まれてしまいます。
1812年、1人の男が間違いだらけの対数表を眺めながら奇想天外なアイデアを思いつきます。「そうだ、数表作成をすべて機械にやらせよう」、そう呟いた者こそ数学者チャールズ・バベッジ(1791-1871)です。
ネイピアが20年を費やして対数表を完成させたのが1614年。それからというもの対数のおかげで数学のみならず諸科学は大きく発展しました。中でも最大のイノベーションは微分積分法です。
連載「人類最高傑作、微分積分はこうして生まれた」でも紹介したように、英国のニュートン(1642-1727)とドイツのライプニッツ(1646-1716)が同時期に発見します。
裕福な資産家の家に生まれたバベッジは、1810年にケンブリッジ大学トリニティ・カレッジに入学します。
学生時代はケンブリッジ大学に浸透するニュートン流微分積分法に反発し、合理的なライプニッツ流を推進し始めるために仲間と解析協会(Analytical Society)を設立するほどでした。のちに、バベッジは37歳でニュートンが座っていたルーカス教授職に就くことになります。
1812年、20歳を過ぎたばかりの青年バベッジの頭脳に浮かんだアイデアが数表自動作成マシンでした。