米航空宇宙局(NASA)が公表した木星表面を覆う雲の画像。1979年の1月と2月にNASAの惑星探査機ボイジャー1号が木星に接近して撮影した白黒画像のネガ3枚を基に作成した〔AFPBB News〕
かけ算がたし算でできる
対数表の数値がどのような方法で計算されているかを見ていく前に、そもそも対数表は何のために考え出されたのかを見ていきましょう。電子計算機が誕生する以前、高度な計算を担っていたのが対数表です。我が国では丸善の対数表が有名です。
現在もなお高校数学の教科書の後ろに対数表は掲載されていますが、使う機会はほとんどなくなってしまいました。
連載「対数の発見がもたらした大航海時代と技術革新」でも紹介したように、対数は天文学的計算を克服するために、城主ジョン・ネイピアによって考案された画期的計算方法です。今から400年前の物語です。
スマートフォンを使いこなす現代人にとって、対数表が電卓代わりになる様子は新鮮に映るはずです。まずは対数表の使い方を簡単な例で理解するところから始めてみます。
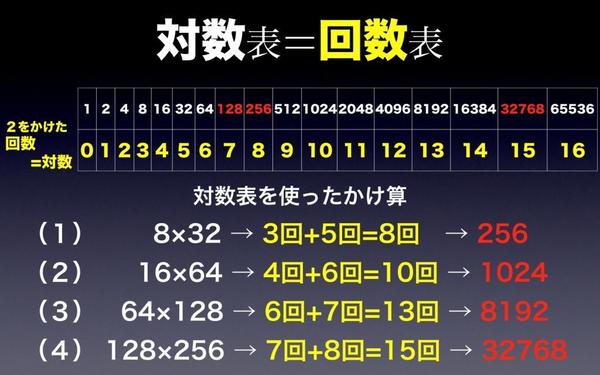
2と2のn乗を表にまとめておきます。下の表では、上の段に2のn乗の値(1、2、4、・・・)、下の段にnの値(0、1、2、・・・)をまとめたものです。この表を用いることでかけ算の答えをあっという間に求めることができます。
例えば、128×256を考えてみます。
まず、128と256を上の段に見つけます。次にその下にあるnの値を確認します。128は7、256は8です。その7と8をたし算します。7+8=15。すると、下の段に15を見つけ、その上の数が求める値になります。したがって、32768が求める積と分かります。
このような数表が対数表です。下の段のnが対数です。128の対数が7であるとは、128=2×2×2×2×2×2×2のように128は2を7回かけた数であることを表しています。
(*配信先のサイトでこの記事をお読みの方はこちらで本記事の図表をご覧いただけます。http://jbpress.ismedia.jp/articles/-/49009)
128×256=(2×2×2×2×2×2×2)×(2×2×2×2×2×2×2×2)
→2を7回+8回=15回かけた数
→対数表から32768
このように、かけ算を計算するのに対数表を用いると、たし算だけで答えが得られるということです。この2のことを底と呼びます。