フォロー
スウェーデン・ストックホルム近郊リンケビーにある中学校の授業風景〔AFPBB News〕
ギャラリーページへ
限りある人生だからこそ
2016年の連載では、円周率、三角関数、対数がいかに探究されてきたのかを紹介しました。連載「ホワイトデーは、アインシュタイン誕生日とπの日」「三角関数が面白くなる4000年の歴史旅行」「対数の発見がもたらした大航海時代と技術革新」参照。
それらの数値がいかに算出されるのか、数が作られる原風景に迫っていきたいと思います。「いかに算出するのか」は電子計算機が発明された現代でさえ重要なテーマとなっています。計算には常に制約がつきまとうからです。
いつの時代も計算は制約の中で行われます。制約の中で、いかに効率良く、いかに速く計算したらいいのか、様々な計算方法が考え出されてきました。
円周率、三角関数、対数の数値計算に進む前に、今回は数値計算の初歩として3つの計算方法を取り上げます。
計算手順の工夫 頭からたし算
手始めにたし算の工夫です。例えば、たし算967+158を筆算で行うと普通は次のように、一の位の桁から桁同士のたし算を行います。
11
967
+ 158
───
1125
普通の筆算（しっぽからたし算）
これを逆に百の位の桁から桁同士のたし算をすることができます。
967
+ 158
───
10
11
15
───
1125
頭からたし算
この筆算方法を「頭からたし算」、普通の筆算を「しっぽからたし算」と呼ぶことにしましょう。2つの筆算の違いはくり上がりです。
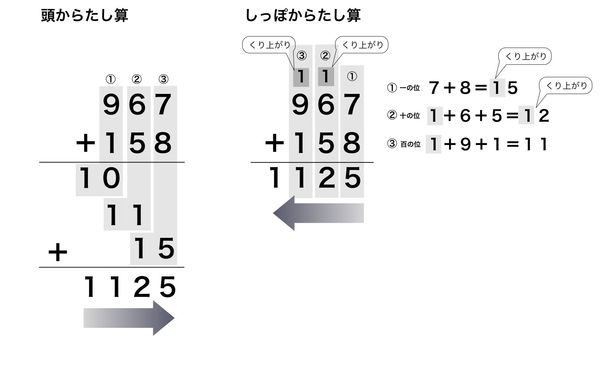頭からたし算と普通の筆算の比較
