銀河「F01004-2237」での潮汐破壊現象を描いた想像図(2017年2月27日提供)。(c)AFP/Sheffield University/Mark A. GARLIC〔AFPBB News〕
Σと∫ デザインの違い
Σの呪縛を解くシリーズも第5弾。今回のテーマは「Σと∫が現れる風景」です。前回「アルキメデスの挑戦」では、曲線の面積を求めたアルキメデスのアイデアを紹介しました。
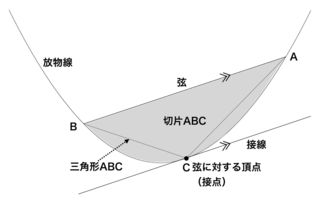
放物線の曲線部分を小さい三角形で分割し徐々に埋め尽くしていく方法で、最終的に三角形の面積の合計が無限級数の和として求められるというものです。アルキメデスの求積法は積分法の原風景でした。
紀元前3世紀のアルキメデスから千年以上の時を経て、17世紀に∫がライプニッツ(1646-1716)によってデザインされます。
記号Σと∫の由来はともに合計SumのSです。ギリシャ文字Σはsigma、積分記号∫はSを上下に伸ばした形です。
数の違いが記号の形に表れています。Σの変数は自然数1,2,3、…です。自然数が1ずつ大きく変化する様子は階段をイメージさせます。それがΣの直角部分とピッタリ。
∫の変数は実数です。実数の特徴は自然数のような離散的ではなく連続的(滑らか)に変化するということです。無限小変化量という考え方です。それが∫の曲線に表れています。∫を使って“曲”の面積を求める求積法が積分法です。
もう1つ、Σと∫に共通していることがあります。どちらも始まり(下端)と終わり(上端)の数で合計が算出される仕組みです。
そこで今回は、Σと∫が同時に現れる風景を2つ眺めていきます。「区分求積法」と「オイラー・マクローリンの公式」です。
Σと∫が現れる風景 その1「区分求積法」
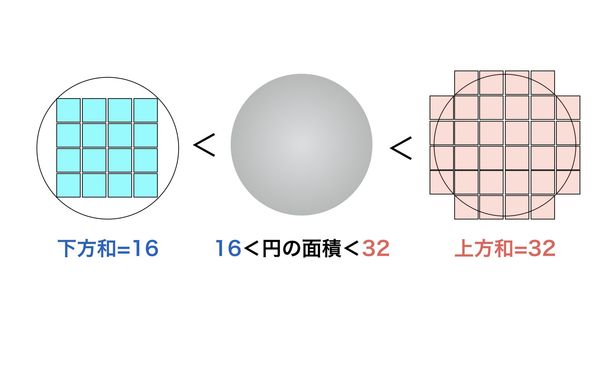
求積において重要な考え方が「下方和」と「上方和」です。これは次の図を見てもらえれば一目瞭然です。
円の面積を考える場合、図のように円の内側に接するマス目の数(面積)と、円の外側に接する円周と交わっているマス目も含めたマス目の数(面積)を比較します。
図の場合のそれぞれ16、32となるので円の面積は16よりも大きく、32よりも小さいことが言えます。このような面積をそれぞれ下方和、上方和と言います。円の面積を下方和と上方和で挟み込んでいるわけです。
円の面積が16より大きく32より小さいとはずいぶん大雑把な見積もりですが、それはマス目が大きいからです。さらに細かい方眼紙で見積もることで下方和と上方和は円の面積に近づきます。
より正確に面積を知るにはよりメッシュを細かくすればいいわけです。かくして、究極に細かく分ければ(分割数を無限にすれば)、下方和と上方和は円の面積に収束します。これが積分法の基本的な考え方です。
前回、放物線の面積をアルキメデスとライプニッツの方法で計算しました。そこで、同じ放物線の面積を下方和と上方和を計算し、分割数を無限にするという極限を取ることで計算してみます。
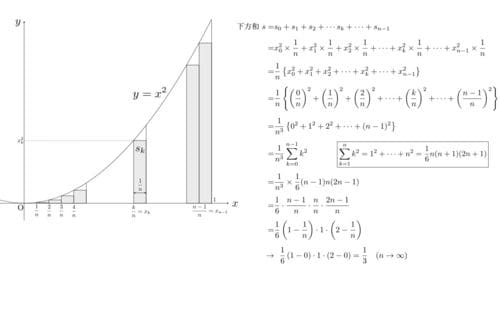
放物線y=x2(y=x^2)とx軸、直線x=1で囲まれた部分の面積を求めてみます。まず、x軸上の区間をn分割(n等分)します。
xが0と1の間の区間(幅1)をn等分すると、分割された一つひとつの幅は1/nです。すると、x=0を0番目のx座標x_0=0、次の1番目のx座標x_1は1/n、…、n番目のx座標x_nはn/n=1と表されます。つまり、k番目のx座標x_kはk/nというわけです。
この準備のもとで下方和sと上方和Sを計算することができます。下方和sは次のように計算され、nを無限大(分割数を無限大)にした極限は1/3と算出されます。
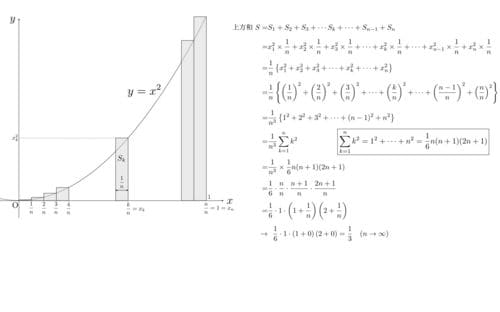
同様にして次の図のように上方和Sも計算できて、極限は1/3と算出されます。