・・・
14枚の画像を見る

Σ（シグマ）公式を振り返る

ギャラリーページへ

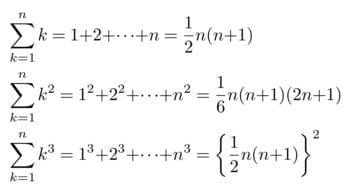
 Σ（シグマ）を見れば、高校時代の数学を思い出す人がいると思います。今回は、この公式の原風景を探ります。

 はたして、そこに現れてくるのが日本人数学者関孝和とオイラーゼータです。

 このΣとは、たし算を簡略化するために考えられた記号です。その特徴は、数列の和であることです。

 数列はナンバリングを添え字で表します。数列の和を表すのに必要な情報は、①変数（ナンバリング）、②初項のナンバリング、③末項のナンバリング、そして④k番目の項を表す数列の一般項の4つです。

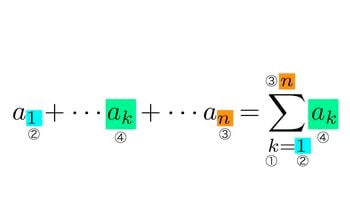総和Σ（シグマ）記号
ギャラリーページへ

 

 Σ記号は総和記号とも呼ばれます。最初の公式に具体的な数値をあてはめて総和が計算される様子を見てみましょう。

 次は100項の数列の和を計算した結果です。Σ記号のおかげで100項すべてを書き出さなくてもいいこと、総和公式のおかげで和はnに100を代入した式を計算すればいいことがわかります。

（＊配信先のサイトでこの記事をお読みの方はこちらで数式をご覧いただけます。http://jbpress.ismedia.jp/articles/-/47000）

ギャラリーページへ

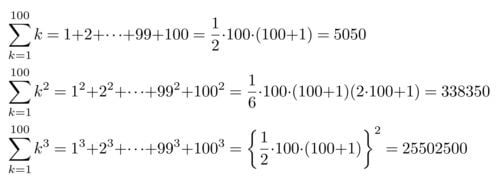
 これがΣの風景です。総和公式とはn項の和をnで表した数式のことだとわかります。

 総和公式のnを∞としたのが無限項の和（無限級数）を表すことになります。オイラーゼータは、一般項が自然数のべき乗の逆数とする無限級数です。

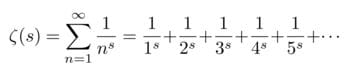オイラーゼータ
ギャラリーページへ

 さて、冒頭Σの総和公式を眺めていると、なぜこのような公式が導かれるのか──証明と、この先の風景を知りたくなります。