 (写真はイメージです)
(写真はイメージです)
(矢原 徹一:九州大学大学院理学研究院教授)
英国のボリス・ジョンソン首相が、流行が収束するまでに人口の60%が感染し、27万人が死亡する予測を発表し、「感染が広がるにつれ、実に多くの家族が身内・親友を失う」という演説を行ったことで、英国だけでなく日本にも大きな不安が広がっています。日本でも多くの人が感染して集団免疫ができるまで流行は収束しないという悲観的な予想を語る識者がいます。しかしその理解は間違っています。
また、日本は諸外国に比べて検査数を少なくすることで実際の感染者を少なく見せているという批判がマスコミで広く報道されていますが、この理解も間違っています。
この記事ではこれらの誤解を正したいと思います。いま行われている検査や現場での対策は、正確な科学的理解にもとづくものです。多くの国民がこの点を理解し、感染拡大の阻止に向けて協力することが、国内における新型コロナウイルス制圧というゴールへの王道です。
感染の動態を記述する方程式
まず、疫学のイロハのイである、「SIRモデル」について説明します。「流行が収束するまでに人口の60%が感染」するという予測はこのモデルにもとづくものです。これを理解せずに感染対策について議論することはできません。現状ではこのモデルについての知識が普及していないため、マスコミやSNS上で不確かな予想が飛び交い、国民の不安を拡大しています。報道関係者、科学者、国会議員、官僚を含むすべての関係者に、このモデルについての基礎知識を持っていただくことが重要と考えます。
SIRモデルのSとはSusceptible(感受性者:ワクチンがない場合は非感染者とみなしてよい)、IとはInfectious(感染性者:感染力のある感染者)、そしてRとはRemoved(除去者=病院に隔離された人+抗体を獲得して感染しなくなった人+死亡者)です。
ある日(t)の、それぞれのグループの人数を、S(t), I(t), R(t)と書くことにします。S(t)人の非感染者と I(t)人の感染者が接触して新規感染者が発生します。その際の感染率をbとします。一方で感染者の一部が病院に隔離されます。隔離される割合(除去率)をcとします。この流れを以下の図にまとめました。
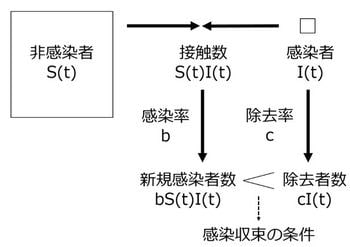
(* 配信先のサイトでこの記事をお読みの方はこちらで本記事の図表をご覧いただけます。
http://jbpress.ismedia.jp/articles/-/59778)
この流れ図にもとづいて、「感染者数I(t)の変化率 I’(t)」は以下の式であらわされます。
I’(t) = bS(t)I(t) - cI(t)
bS(t)I(t)はその日に新たに感染する人の数、つまり「感染者増加率 S’(t)」です。cI(t)はその日に新たに除去された人の数、つまり「除去者増加率 R’(t)」です。
I’(t) = S‘(t) - R’(t)
この式の差し引きがマイナスになれば、感染は収束に向かいます。したがって、感染対策の目標は、S‘(t) < R’(t) という状況(感染者増加率より除去者増加率が大きい状況)をできるだけ早く実現することです。












