生涯二度と忘れないでしょう。そういう教育が私は好きだし、もっぱらそういう講義演習・レッスン・リハーサルしかしない、を自身の生活原理として律しています。
さて、それでいま上に書いた2番目の式、これは、本当は数値a、v、xなどをたて、よこ、おくゆきの番地が揃った数の組で表してやる方が一般的だし、そうでないと現実には使い物になりません。
というのも、私たちは3次元空間で生活していることでもあるし、世の中の運動は一般に1次元上のみに限られるわけではないからです。
そういう数の組をベクトルと呼び、F、a、v、xに対応する多次元の所番地すなわち
力をベクトルF
加速度ベクトルa
速度ベクトルv
位置ベクトルr (これだけ文字が違うのは、(x、y、z)と3つ成分のある3次元の所番地をrで代表させているのですが、これらの表記を使って
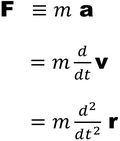
と記すと初めて現実の系(例えば糸巻き戦車でも何でもいいんですが、糸巻き戦車は十分に複雑な系になります)の運動を記述できる入口に立ちます。これは大学1年前期の程度になります。
そこで、このように書くと初めて、ああ、力の向きは加速度の向きと同じなんだな、といった現実の時空間における物体の運動の軌跡と力の向きが、生き生きとまたありありとイメージできるようになり始めます。
(この時点ではいまだ質点という仮想的なモデルですが、中学生向けの文字式で、それを想像せよ、というのは、むしろ酷な話です)
こういうものを使う回は、ビューが極端に伸びなかったり、逆に伸びたりするので、今回はどちらに振れるかなと案じてもいるのですが・・・。











