フォロー
バチカンでハンガリー国立フィルハーモニー管弦楽団の指揮を執るハンガリーの指揮者ゾルタン・コチシュ氏〔AFPBB News〕
ギャラリーページへ
冨田勲「宇宙幻想」の思い出
「フーリエ級数」、私がその数学用語を初めて目にしたのは14歳、数学書ではなく音楽アルバムのライナーノーツでした。それが冨田勲（1932-2016）の「宇宙幻想」（1978年、LP）です。冨田はシンセサイザーという電子楽器の仕組みの解説を次の数式とともに始めたのです。
（＊配信先のサイトでこの記事をお読みの方はこちらで本記事のグラフや式をご覧いただけます。http://jbpress.ismedia.jp/articles/-/48349）
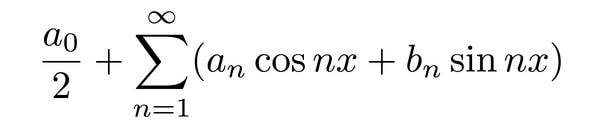フーリエ級数（三角級数）
・・・
12枚の画像を見る
シンセサイザーは、正弦波（サイン波）を重ね合わせることで多種多様な音源を作り出す電子楽器であること。その数学的表現が「フーリエ変換」であると述べられていました。
18世紀、数学者フーリエの主張は次の通り。
任意の関数は三角関数の無限級数（フーリエ級数）で表すことができる。
これがフーリエ変換です。次のように言い換えることもできます。
任意の曲線は正弦波と余弦波の合成で表すことができる。
シンセサイズは「合成する」の意味です。「合成装置」を意味する「シンセサイザー」は、電気的に作り出された波形を重ね合わせることで様々な音を「合成」する楽器という意味です。
直線をサイン波で表す
百聞は一見に如かず。例として直線f(x)=xがサイン波の重ね合わせ（たし算）で表される様子を眺めてみます。まずsinを10項たし算した場合のグラフです。グラフは波打っているのが分かります。
ギャラリーページへ
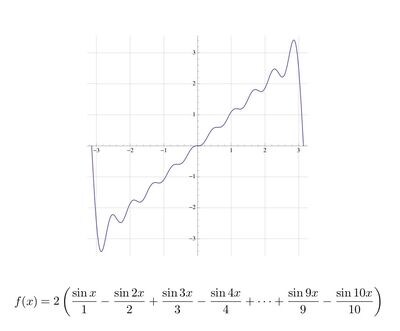
次にsinを100項たし算してみます。グラフは両端付近以外では直線に見えます。
ギャラリーページへ
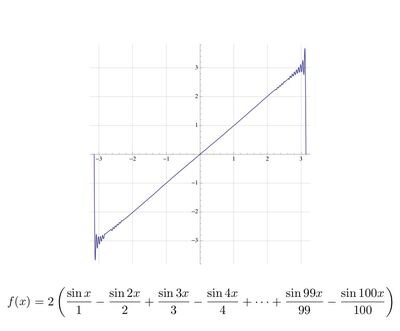
このように重ね合わせの数（sinの項数）を大きくしていくと直線に近づいていく様子が分かります。
