数学を駆使して作られる巨大数

天文学的数字と人は言う・・・。写真は地球から約20光年離れた距離にある赤色矮星（わいせい）のグリーゼ581の惑星系。手前は惑星グリーゼ581g。NASA提供の想像図〔AFPBB News〕

ギャラリーページへ

少ない記号で大きな数を表す方法

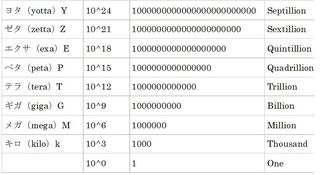
 無量大数は68、Millinillion（ミリニリオン）は3003、不可説不可説転は37218383881977644441306597687849648128。これらは前回の連載「大きな数の単位を作ってきた人類」（http://jbpress.ismedia.jp/articles/-/48053）で紹介した数の単位と1の後に続く0の個数です。

 これら数の単位はある数の大きさに漢字やアルファベットで構成された1つの単語が対応するものです。

 不可説不可説転よりも大きな数を表すには新たな単語をどんどん作っていく方法が考えられますが、不可説不可説転のようにその単語は7文字の漢字でできていても、1の後に続く0の個数を数字で表すのが容易ではありません。漢字やアルファベットだけによる表し方には限界があります。

 そこで数学の出番です。数字と演算記号を用いることで容易に大きな数を作り出すことができます。演算を定義していきます。演算の基本はたし算（加法）です。たし算することでより大きな数を作り出すことができます。

 次にたし算をまとめた演算として定義されるのがかけ算（乗法）「×」です。a個のbのたし算をa×bもしくはb×aと表します。

999×999＝998001
かけ算（乗法）「×」

 右辺の6桁の数998001を表すのに999×999と7文字を用いています。

 さらに、かけ算を“かさねる”演算として定義されるのが累乗（冪乗）です。累とは、かさねるという意味で、冪（べき）とは、おおいかぶせるという意味です。aをb回乗じることをaのb乗といい次のように表します。

a^b=a^b=a×…×a
累乗（べき乗）aが底、bが指数

 累乗によって大きな数を少ない文字数で表すことができます。

9⁹=9^9=387420489

 指数表記ならば9桁の数387420489を表すのにたった2文字しか用いていません。

3つの数字だけで表すことができる最大の数は？

 答えは「9の（9の9乗）乗」です。

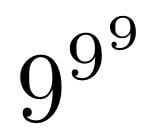9の（9の9乗）乗（9^(9^9)）

・・・

6枚の画像を見る

 9の9乗が387420489ですから、この数は、9の387420489乗です。9の9乗ならば電卓でも可能ですが、9の387420489乗は電卓では計算不可能です。

 ならばコンピューターを使ってみましょう。実はコンピューターでも手に余る計算です。計算用ソフトウェアを準備しなければならないからです。試しに現代の数学ソフト「Mathematica」で9の（9の9乗）乗を計算させてみます。結果は次の通り計算できる大きさを超えていますと叱られてしまいます。

「計算中にオーバーフローが起こりました」