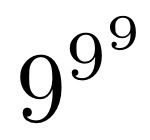インドネシア・バリ島のジンバランで、パラグライダー同時飛行の世界記録更新に臨む人たち(2016年10月16日撮影)〔AFPBB News〕
連載に登場した微分方程式
数学の威力はその汎用性にあると言えます。
湯飲み茶碗のお茶やお風呂の温度、薬の吸収、マルサスの人口論、ラジウム(放射性元素)の半減期、うわさの伝播、アルコールの吸収と事故危険率、人工肝臓器、水中で吸収される光量、そして肉まんの温度、これらの異なる現象がすべて1つの数式で説明することができることを連載「人類最高傑作、微分積分はこうして生まれた」で紹介しました。
同じように、交流回路(LC共振回路)とバネの振動という異なる現象も同じ数式で説明できることは連載「電気とともにある数学」で紹介しました。
このようなモデリングに用いられる数式が「微分方程式」です。微分法とは、刻々変化する様子、すなわち運動を定量化する高度な技であり、積分とは刻々の変化を集積する技のことです。
無限に分割したものを無限に足し上げる“スーパーたし算”が積分法であることを連載「人生を積分して知る驚きの結果、大学生は早下り坂」で紹介しました。
微分積分=小石?
大昔、数字がまだなかった時代、私たちは飼っている動物を数えるのに小石を使っていました。小石を意味するラテン語が「calc」です。カルシウム(calcium)の「calc」です。これが「calc=計算」の由来です。
「calculate」は「計算する」、「calculator」は「計算機」、「pocket calculator」は「電卓」です。そして、「calculus」は「計算法」を意味しますが、これには「微分積分法」の意味もあるのです。
微分法と積分法はまさに計算法です。それも曲者である“曲”を計ることができる最強の計算技術が微分積分「calculus」なのです。人類が「曲=運動」をいかに理解しようとしてきたのかを振り返っていきます。
アリストテレスの運動論
微分方程式はそもそも「運動」を考えることを発端にしています。何が運動を起こさせる原因なのか、運動する先にどんな未来があるのかという運動の過去と未来を語るために運動それ自体の本質を研究することが古代ギリシャ時代からなされてきました。
アリストテレス(前384-前322)は身の回りの運動を注意深く観察することで、力と運動の関係を考えました。物の本性は静止であり、運動している物体には絶えず力が働いているという結論を下しました。
アリストテレスは運動を2つに分類しています。力が物体に内在するために自然に生じる運動(自然運動)と、他から力が加わって生じる運動(強制運動)です。
自然運動の代表例が物の自由落下運動です。物が下へ落ちる理由をアリストテレスは次のように説明しました。
物が自分にとっての"自然な"場所である地球の中心に落ち着こうとする運動が自由落下運動であり、あたかも家にたどり着こうとする人の足取りが自分の家に近づくにつれて速くなるように、物もまた"自然な"場所に近づくほど速くなるのが加速する理由であると。