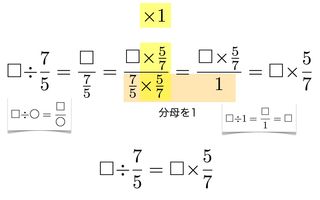
連載では9にまつわる話題をいくつも取り上げてきました。9の段の九九の特別な方法と9の倍数判定法、ジョン・ネイピア対数誕生物語(底が0.9999999)、ネイピア数e誕生物語などですが、どれも9が特別な役割を果たしています。
9の倍数判定法
ある数の桁の和が9の倍数であれば元の数は9の倍数とわかります。これは桁の和はある数を9で割った余りを表していることによります。
123÷9の余り 1+2+3=6 → 123は9の倍数でない
345÷9の余り 3+4+5=12 → 1+2=3 → 345は9の倍数でない
8973÷9の余り 8+9+7+3=27 → 2+7=9 → 8973は9の倍数である
合同式(mod)を用いた証明は連載で紹介しました。
さて、今回は9の倍数判定法の応用を紹介していきたいと思います。
9去法(きゅうきょほう)
9の倍数判定法を検算に応用することができます。まずは具体例を見てもらいましょう。
349+637+273=1259という計算を検算する場合、次のように両辺の桁から9または和が9の桁部分を除き、さらに残った桁の和を求め最後に1桁にします。この場合、左辺は3つの1桁の数を合計し、桁の和を求め最後に1桁にします。
はたして、両辺とも最終1桁の数が等しければ、たし算は(たぶん)合っている、等しくなければ誤っていることがわかります。
349 →桁に9があれば除く→34→和3+4=7
637 →和が9の桁63を除く →7
+273 →和が9の桁27を除く →3
合計7+7+3=17→1+7=8
─────────────────────────────────
1259 →桁または和が9の除く→125→和1+2+5=8
この問題の場合、ともに8で等しいので(たぶん)合っていることがわかります。
たぶんといったのは、右辺が正答1259でない場合でも最後の1桁が8になる数があるからです。ちょうど9の倍数だけまちがっている場合には最後の1桁は等しくなります。例えば、次のような計算です。最後の1桁が8で等しくても計算は誤りです。
349+637+273≠1106
349 →桁に9があれば除く→34→和3+4=7
637 →和が9の桁63を除く →7
+273 →和が9の桁27を除く →3
合計7+7+3=17→1+7=8
─────────────────────────────────
1106 →和1+1+0+6=8
正答と誤答の差1259-1106=153(9の倍数)
このような、計算過程で9を除いていく四則の検算方法が9去法と呼ばれるものです。9去法による検算は計算誤りだけは確実に判定できる「計算まちがい判定法」です。
ひき算、かけ算の場合も同様に、左辺部分をそれぞれひき算、かけ算して最後の1桁を求めることで検算できます。わり算はいったんかけ算に直すことで検算できます。