前回は「日本の折り紙が「古代ギリシャ3大難問」幾何の作図問題を見事に解決」(https://jbpress.ismedia.jp/articles/-/71457)という、およそのどかで教育的な話題を取り上げました。
「夏休み親子向け」といっても、それほどアクセスは期待できないだろうと覚悟していたのですが、予想に反して大きな反響をいただきました。
そこで、その続編をお届けします。
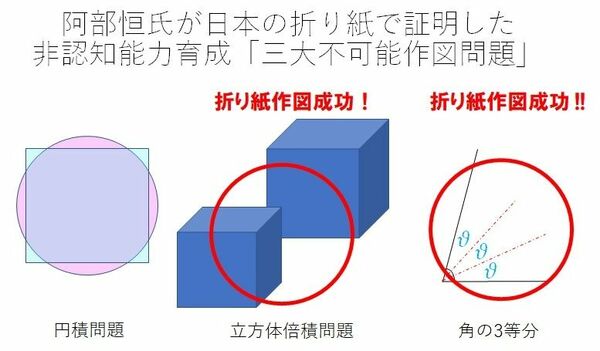
「角の3等分」「立方体倍積問題」という古代ギリシャの「作図不可能問題」2つを「折り紙」で解決された阿部恒さん(1929-2015)は1980年に雑誌「数学セミナー」の表紙で、革命的といえる「折り紙幾何学」による証明を公開されました。
しかし、その経歴などは当初、よく分かりませんでした。
多くの著書の略歴には「元折り紙協会事務局長」(https://www.nippyo.co.jp/shop/author/572.html)などとあるだけ。
でも古代ギリシャの3大幾何学難問を解くというのは、ただ事ではありません。
塩野直道畢生の「小学算術緑表紙教科書」(1935-43)で最初から最後まで学んだ、日本史上「算数最強」世代の一番上の学年に当たり、ただものではないことはすぐに分かります。
そこで、可能な限りの著書を取り寄せてみたところ、今風な派手さが一切ない、昔風の優しい、珠玉のような「お母さんと折るおりがみ」(サンリオ1981/92)から、状況が分かり始めました。
この本の版元でもあるサンリオに「遊びの部屋」という部署があり、阿部さんはそこに1970年前後に着任。
「20年近くの間、全国各地で行われる子供のためのイベントに参加」され
「おりがみ教室を開いたりして」
「日本固有の文化の一つであるおりがみを子供たちにつたえ」
「そのなかでおりがみの素晴らしい効用を発見し」
「思いもよらなかった子供たちの生の反応を経験」された、現場叩き上げのプロという横顔をお持ちだったのです。