4枚の画像を見る

9の段だけの特別な方法！

 本連載第2回は両手の中に九九の計算が隠れていることを紹介しました。

 そのときの例題は8×9＝72でしたが、8×9＝9×8なので、9の段の九九とみることができます。9の段の九九には、この前とは別な計算方法があります。両手を用いることは同じです。

 まず手の裏を自分に見せて両手を開きます。

 9×3であれば、左から3本目の指を内側に折り曲げます。すると、折り曲げた指の左側に立っている指の本数2が積の十の位、右側に立っている指の本数7が積の一の位の数を表します。9×3＝27の2と7が同時に指の本数として見えているということです。

 9×8であれば、左から8本目の指を内側に折り曲げます。すると、折り曲げた指の左側に立っている指の本数7、右側の立っている指の本数2なので、9×8＝72と分かります。

九の段を眺める

 実はこの両手を使った方法は九九がない米国でよく知られたものです。その仕組みを謎解いてみましょう。

 まずは、九九の九の段をじっと眺めてみます。

ギャラリーページへ

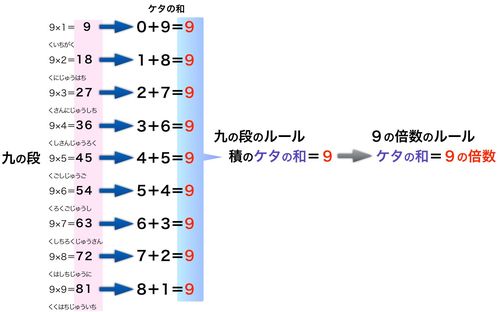
 右辺の積にある"事実"――。どれもケタの和が9であることに気づくでしょう。この事実を両手を用いた方法に表現し直したということです。

 両手の10本の指のうちどれか1本の指を折れば、残りは必ず9本です。

   十の位 ｜ 一の位 
9×3＝（3－1）｜（10－3）
  ＝   2   ｜  7

   十の位 ｜ 一の位 
9×a＝（a－1）｜（10－a）
   （a－1）＋（10－a）＝9

 このことから左からa本目の指を折れば、十の位（a－1）は折った指の左側の指の本数、そして一の位（10－a）は折った指の右側の指の本数に等しいことが分かります。

 Aの範囲は1から10まで当てはめると次のように9×10＝90まで表すことができます。