ネイピア数eの威力
2.71828182845904523536028747135266249775724709369995・・・
人類のイノベーションの中で最高傑作の1つが「微分積分」です。冒頭の数がその巨大な世界の礎となり、土台を支えています。この数は、ネイピア数eまたは自然対数の底と呼ばれる数学定数です。
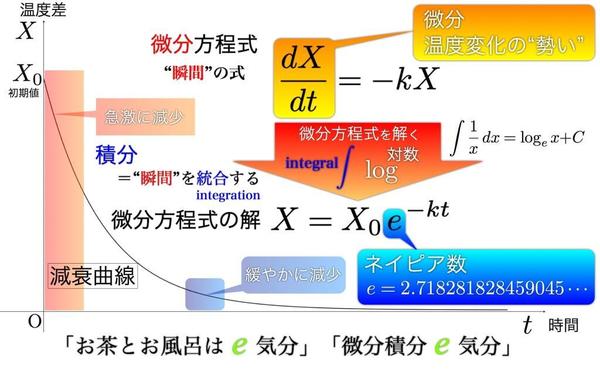
湯飲み茶碗のお茶やお風呂の温度、薬の吸収、マルサスの人口論、ラジウム(放射性元素)の半減期、うわさの伝播、アルコールの吸収と事故危険率、人工肝臓器、水中で吸収される光量、そして肉まんの温度、これらすべてが次の数式によってうまく説明できます。
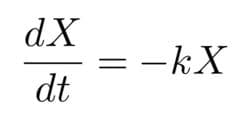 微分方程式
微分方程式
これが「微分方程式」と呼ばれるものです。たった1個の数学モデルでさまざまな世界の多様な状況を表現できることは驚きであり歓びでもあります。
例えば、湯飲み茶碗のお茶の温度とそれが置かれた室温の温度差をX、時間をtとすれば、式の左辺(微分)は「温度変化の勢い」を表します。すると、微分方程式は、温度変化の勢いが、温度差Xに比例(比例定数k)することを表しています。kにマイナスが付いているのは、温度が下がることを表します。
入れ立て時は、お茶の温度は熱くXの値は大きいので、温度の下がる勢いも大きくなります。時間が経ってお茶の温度が下がった時にはXが小さいので、温度の下がる勢いも小さくなります。
お茶の温度は入れ立て時に急減に下がり、時間が経った後ではゆっくり温度が下がることを私たちは経験で知っていますが、そのことを表したのが微分方程式です。微分とは刻一刻変化する様子を表す言葉です。
ある時刻、その瞬間における温度の下がり方の勢いがどのように決まるのかを表したのが微分方程式です。
さて、方程式は解くことができます。微分方程式を解くと次の解が得られます。
温度X=(時間tの式)
微分方程式の解
したがって、縦軸を温度、横軸を時間とするグラフを描き、温度変化を一覧できるようになります。
では、この微分方程式がどのように解かれていくのか過程を追ってみましょう。