著者フォロー
OpenClipart-VectorsによるPixabayからの画像
時折ネット上で目にする、何らかの教育が「不要」と主張する根本的な誤りにはいくつかのパターンがあります。
よく目にするのは「中学で教える図形問題。高校以降全然使わず、無駄だから廃止すべき」といった短見。
つまり、何らかの教程が「必要ない」「いらない」と思い込んでいるパターン。
これがどれほど大間違いであるかを、本稿では示したいと思います。
最初に、読者の皆さんに一つクイズを出しましょう。
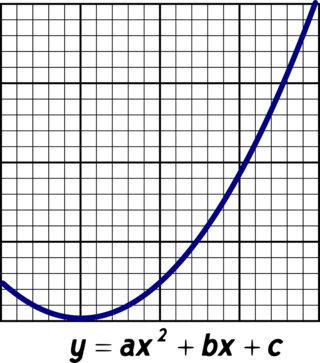
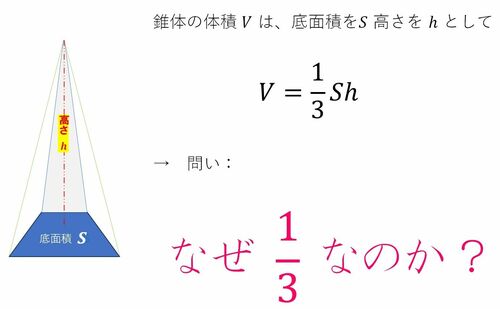
「小中学校の算数・数学では三角錐や四角錐の体積は1/3×底面積×高さと教えます。なぜ1/3なのか？ 小学生に分かるよう、平易に説明（証明）してあげてください」
もし子供に質問されたら、皆さんどのようにお答えになりますか？
生活経験のないものは認識が困難
中学数学で「図形は無用」を主張する人の意見を見てみると、しばしば「方程式や微分積分は大学受験でも使うけれど、図形は使わない」というんですね。
でもそれは、「公式」を暗記してテストなどを通過し、まともに数学と関わらなかったと告白しているのに等しい。
それが何より証拠には、「積分」の「積」は「面積」「体積」の積で、図形そのものではないですか。
実際、分かっている人でも上の「3分の1」クイズを微積分で答えようとする人（理系の大学生など）がいます。
そういう時には、「小学生に分かるようにしてよ。そもそも卑弥呼よりはるか昔、古代ギリシャでも証明してたんだから、日本なら江戸時代のニュートンやライプニッツが発明した微積分は必要ないでしょう？」と、考えてもらいます。
中学の幾何が高校以降必要ない？
いえいえ、とんでもない。それは知らないだけのことで、受験でも例えば東京大学の2次試験は、数Ⅰの空間図形が一番難しく、数Ⅲでも回転体の体積などが頻出します。
なぜでしょう？
第1に、かつてはあらゆるエンジニアが「製図」する必要がありました。私が学部学生だった1980年代は、工学部進学希望者には「図学」が必修。
これが1990年代にCAD（Computer-Aided Design、キャド）のマシンに置き換わり、「図学教室」も「情報図形教室」に様変わりした。
私は情報図形の学内非常勤として「全学必修・文理共通・情報処理」を担当していました。
大学、大学院、実社会に出て以降の、メカニズムを扱うあらゆる専門で、幾何的なアナロジー＝類推が決定的に重要になります。
もし図形の勘が働かないと、ベクトル解析でも力学でも統計力学でも、機械学習の基礎の理解に著しい困難が立ちふさがります。
例えば、エレクトロニクスの基本である「電磁気学」。
電場、磁場などの概念が出てきますが、誰も「でんば」を見たことがある人はいません。
「じば」の方は、棒磁石と砂鉄などを使って様々な可視化が可能です。
そこで、こうしたものを一度見て体験、理解すれば、これと似たものをイメージするのは容易です。
こうした「原体験」を生活環境で持たせ、そこから類推＝アナロジーを働かせることで、様々な抽象的概念を、発達段階にある子供たちは獲得することができるようになります。
