3回にわたり語ってきた超入門リーマン予想もこれが最終回です。リーマン予想を語るための数式はこれまでの連載の中に登場済みです。最終回は数式は最小限にしました。最後まで一気に文章を読んでいただきたいと思います。
リーマン予想とは、ゼータ予想のことに他なりません。オイラーによって発見された最初のゼータ関数(オイラーゼータ、連載)。その定義域は、自然数から始まって実数まで拡張されました。その仕事がオイラーの偉業です。
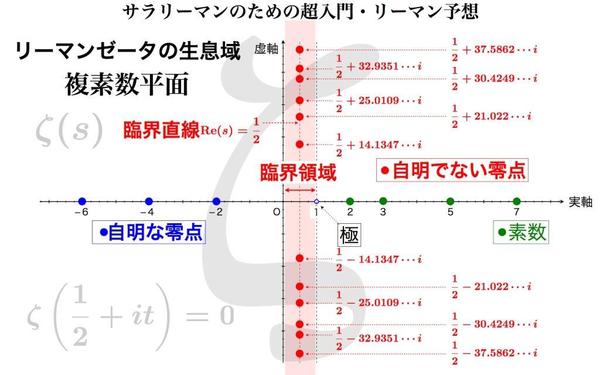
その次の仕事がリーマンによるゼータ関数(リーマンゼータ)です。その定義域は複素数にまで拡張されました。
それが前回に紹介した解析接続と呼ばれる方法です。オイラーゼータに対して解析接続したのがリーマンゼータです。
リーマンは複素数の世界で生息するゼータを発見し、その挙動を探ります。
そもそものきっかけは素数の個数を精確に表す公式をつくることでした。
連載で紹介したように、オイラーはオイラーゼータが素数と密接に関係していることを解明していました。
リーマンは、複素数に生息するリーマンゼータと素数の関係を考察することで、素数の個数を表す素数公式を発見するに到りました。
この研究の中でリーマンが捕らえたのがリーマンゼータの零点です。関数f(x)の零点とは、方程式f(x)=0のxのことです。
リーマンゼータの零点αとは、
ゼータ方程式 ζ(α)=0
の複素数αのことです。