皆さんに次のような経験はないだろうか。

　上役が取引先のパーティーに呼ばれていたが、急用で行けないため、代役を頼まれた。一流ホテルでの数百人規模のパーティーだが、自分が知っている人は誰もいない。会場は混雑しており、隣の男とぶつかってしまった。これがきっかけで、その人と世間話を始める。すると、最初赤の他人と思っていた彼が、妻の中学時代の同級生の夫と分かった。

　こうした体験を、よく「世間は狭い」という。英語圏では「スモールワールド（small world）」、専門的には「6次の隔たり」として知られる。先の例だと、自分と妻の間は、直接知っているから1次の隔たりであり、妻の中学同級生との間は2次、その夫とは3次の隔たりである。このように数えていくと、世界中の誰とも、ほぼ6次の隔たりでつながっていることが、経験知として知られている。

　重要なことは、赤の他人と思っていた人が、わずか数人の知人を介して、数次の隔たりでつながっており、そういった「遠くの知人」こそが、転職や開業など人生の転機で、ウマイ話を運んできてくれる可能性が高いことだ。

　というのも、そうした遠くの人は、自分の生活圏から離れた場所で活動しており、こちらの活動圏では得られない情報をふんだんに持っているからだ。

「遠距離交際」と「近所づきあい」

　こうした経験則は、1960年代以降、米国のスタンリー・ミルグラム、マーク・グラノベッター、ロナルド・バートらの研究によって深められた。

　90年代に入ると、パソコン性能の飛躍的向上もあってシミュレーションが簡便に行えるようになり、ダンカン・ワッツらをはじめとする応用数学や物理学系の学者によって、それまで直感的、経験的にしか把握されてこなかったスモールワールドネットワークに、理論的な根拠が与えられた。

　その分析ツールは、グラフ理論である。グラフ理論とは、森羅万象の関係性を、点（ノード）と線（リンク）のつながりに着目して考究しようとする数学の一分野であり、ノードとリンクで表現可能なものすべてが研究対象となる。

　例えば、論文の共著者関係や送電網、ハリウッドスターの共演者関係、線虫の神経ネットワーク、言語連想などである。

　ワッツらの研究は、一見バラバラな現象のように見えるこれらのネットワークの振る舞いを、単純で普遍的な原理で説明する可能性を開き、幅広い影響力を持った。

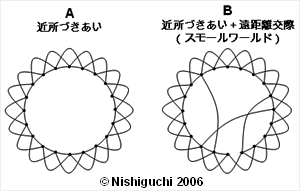図1　遠距離交際と近所づきあいのネットワーク。点は「個人」、線は「つながり」を示す
ギャラリーページへ

　図1は、「遠距離交際」と「近所づきあい」のネットワークを表す（筆者の用語）。図左Aの任意の点は、直近の隣どうし、および、隣の隣とつながっているのが分かる。これは、近所づきあいの関係である。

　例えば、図の円を地球と考え、自分の地点から地球の反対側に、伝言ゲームで情報伝達するとしよう。Aの近所づきあいだけのネットワークでは介在者が多すぎて、途中で情報が逸失するか、誤って伝わってしまう。

　図にはないが、つながり方にまったく法則性がないものは、「ランダムネットワーク」と呼ばれる。この場合、地球の反対側の「ターゲットパーソン」に情報を伝えようとしても、その伝達特性や可能性はまったく予測できず、伝達効率も無に等しい。