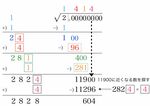
最後に√の中の小数点「.」を√の真上に書いて√2の近似値が「1.4142」と求まります。
この開平法は最初の当たりをつける計算法に比べて2乗の計算を必要としないだけ効率は良くなっていますが、√2の値が1桁ずつ算出されていく様子は変わりありません。
ニュートン法
そして3番目のニュートン法です。これまでの2つの計算方法と大きく異なるのがスピードです。
いかに速く√2の近似値が算出されるのかを見ていただきましょう。
√2という数は方程式x2=2のxを満たす数です。すると関数y=x2-2のグラフのx切片(グラフとx軸の交点)を√2と見ることができます。
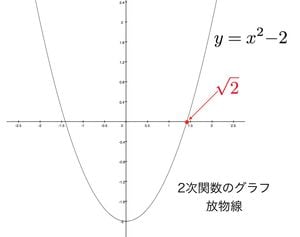
まず、放物線上のx切片でない適当な1点を選びます。そのx座標をx1として、その点を接点とする接線を求めます。次に、この接線のx切片(x軸との交点)をx2とします。
同じように、y=x2である放物線上の接線を求め、この接線のx切片をx3とします。このように接点、接線、x切片xnを逐次求めていくとき、x切片xnが√2に限りなく近づいていきます。
曲線の接線の方程式を求めるときに活躍するのが微分法です。連載「運動を語る言葉、「微分」の正体」では、「微分=勢い」であることを説明しました。曲線における微分(=勢い)とは接線の傾きを表します。
関数xnの微分はnxn-1と計算されます。この公式を用いて関数y=x2-2の微分は2xとなります。すると、接点のx座標がx=xnにおける接線の方程式が求まります。
接線の方程式でy=0としてx切片が得られます。このx切片は次の接点のx座標となるのでxn+1と表します。xnとxn+1の関係式を用いることで、接点のx座標xnは初項x1からx2、x3、x4、…と算出されていきます。
実際の計算過程は次のようになります。

この計算結果をグラフに表してみると接点のx座標が√2に近づいていく様子が鮮明に分かります。
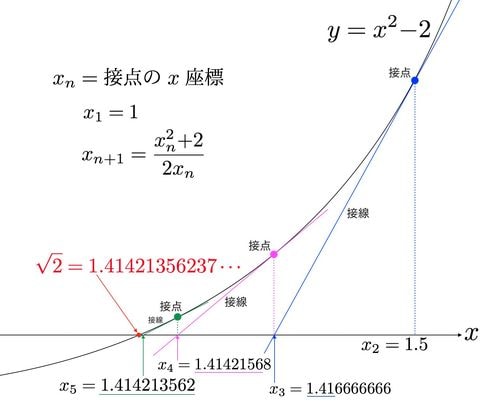
x1=1
x2=1.5
x3=1.416666666
x4=1.41421568
x5=1.414213562
√2=1.41421356237…
これだけのステップで√2の小数点以下9桁まで正しい数値が算出されます。これが最初の2つの計算方法にはないスピードです。放物線という曲線を使うことで√2の近似値が速く得られることに驚くばかりです。
前回の最後でも述べたように、微分積分法がcalculus(計算法)と呼ばれる理由が、数値計算に対する威力にあります。
まっすぐな直線を測ることは容易ですが、曲線を測ることは困難を極めます。人類は長い時間をかけてその困難を克服しました。その超絶技法こそ微分積分法なのです。
微分積分について語ったこれまでの連載「人類最高傑作、微分積分はこうして生まれた」「人生を積分して知る驚きの結果、大学生は早下り坂」も併せてお読みください。