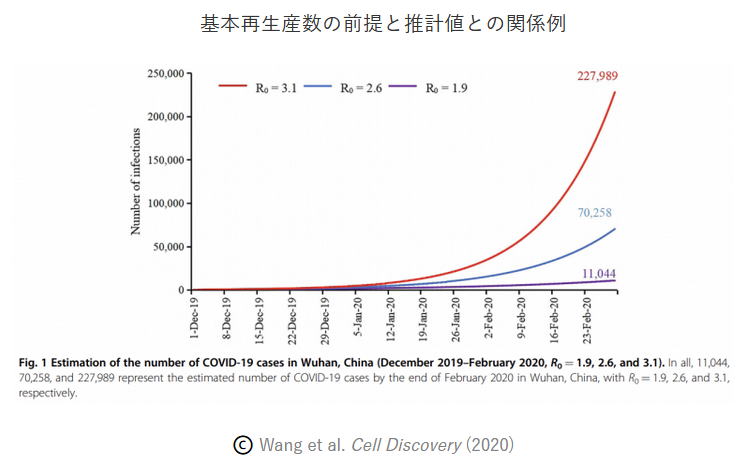
シンプルなモデルを手掛かりに
感染症の動向を予測するための、よく知られるシンプルなモデルは、「SIR モデル」と呼ばれるものです（モデルの概要にご関心のある方は、後述の別添をお読みください）。
このモデルでは、先行きの感染者比率は、現時点での「非感染者比率」に「感染者比率」を乗じ、さらに「基本再生産数」を乗じたものに左右されると捉えられます。この「基本再生産数（Basic Reproduction Number, R0と表されることが多い）」とは、「免疫を持たない集団に入り込んだ感染者1人が、回復するまでに何人に感染させるか」を示す値です。この値は、病原体そのものの感染力や、人と人との接触頻度によって決まります。
また、「非感染者比率」と「感染者比率」を乗じるのは、直感的にも理解しやすいでしょう。非感染者比率が100％（すなわち、感染者がゼロ）なら感染は起こらず、一方で、非感染者比率が0%（すなわち、全員が感染済み）になってしまうと、もうそれ以上感染は広がりようがないからです。
この基本再生産数が1を大きく上回れば、新たに増えた感染者が、非感染者をさらに感染させやすくするため、急速に感染が広まりやすくなります。一方で、基本再生産数が1を下回れば、計算上、感染は徐々に収束していくことになります。
（なお、「免疫を持たない集団」ではなく、すでに感染者が出ている環境での特定の時点tにおいて、感染者一人が何人に感染させるかを示す値は、「実効再生産数（Effective Reproduction Number）」と呼ばれ、Rtと表されます。これも感染抑制にとって重要な目安となる値ですが、この値は時点によって変動するため、議論をシンプルにする観点から、本稿では「基本再生産数」に絞って記述することとします。）
したがって、「基本再生産数が1を下回る所まで人と人との接触を減らそう」と考えることは、対応としては自然です。しかし、現実の政策判断においてどの程度の行動制限をかければ良いのか、モデルから導き出すことは容易ではありません。
経済分析に長らく従事し、さまざまなモデルを見てきた立場からみて、このモデルの特徴は「基本再生産数」に推計値が大きく左右される点にあります。
基本再生産数が既知、かつ不変であれば良いのですが、現実のウイルスは変異を繰り返します。この結果生じる「基本再生産数」の振れと不確実性は、そのまま推計値に大きな不確実性をもたらします。したがって、ここから導き出される推計値は、本来、相当な幅をもってみるべきものです。
政策対応の経済への影響
そのうえで、最近よく分析に使われる、レストラン予約サイト“Open Table”のレストラン予約状況から、政策対応との関係を見てみましょう。これを見ると、国によって対応はかなりまちまちであり、また、どの国の対応が優れているとも言い切れないことが窺われます。
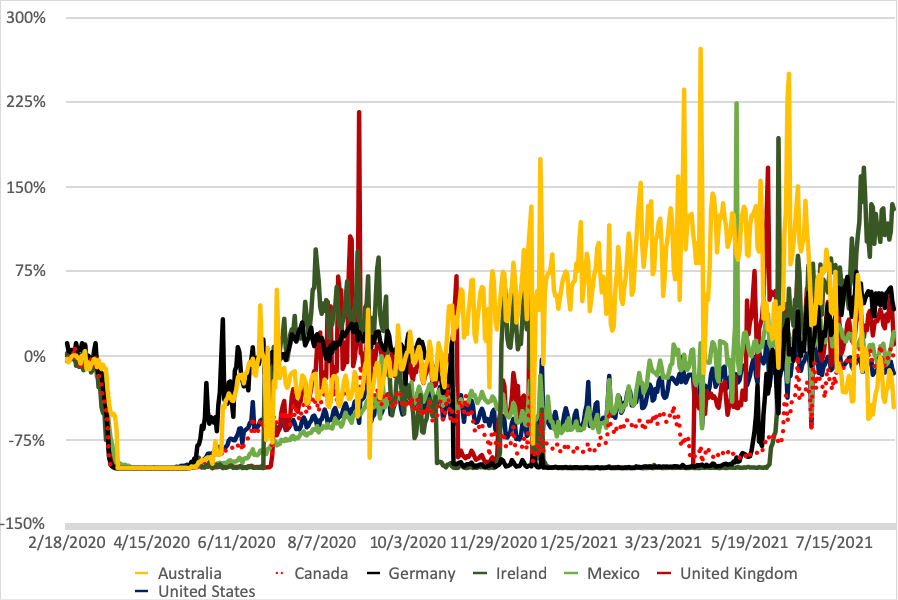“Open Table”によるレストラン予約件数前年比出所：Open Table（異常値を一部筆者が修正）
